← Feed
Academy
ทำไมการเปลี่ยนใจถึงมีโอกาสชนะมากกว่า? (Monty Hall problem)
Shironne
Author

Monty Hall problem หรือ ปริศนามอนตี ฮอลล์ เป็นปริศนาทางความน่าจะเป็น โดยปริศนามาจากชื่อพิธีกรในรายการโทรทัศน์หนึ่งของอเมริกาที่มีชื่อว่า Let's Make a Deal ซึ่งเป็นเกมโชว์ทางโทรทัศน์จากสหรัฐอเมริกา ออกอากาศครั้งแรกในปี 1963 และมีพิธิกรที่ชื่อ "มอนตี ฮอลล์" เป็นผู้ดำเนินรายการ
ในรายการผู้เข้าแข่งขันจะได้เลือกประตูหนึ่งในสามบาน โดยมีรางวัลใหญ่เป็นรถยนต์อยู่ข้างหลังประตูเพียงบานเดียว ส่วนอีกสองบานมีแพะอยู่ มอนตี ฮอลล์ในฐานะพิธีกรซึ่งรู้คำตอบ จะเปิดประตูที่ไม่ได้ถูกเลือกและมีแพะอยู่เสมอ แล้วจึงถามผู้เข้าแข่งขันว่าจะเปลี่ยนใจเลือกประตูที่ยังปิดอยู่หรือไม่ ดังตัวอย่างต่อไปนี้


ผู้เล่นเลือกบานที่สอง พิธีกรจึงเปิดประตูบานหนึ่งที่มีแพะ
ปริศนานี้กลายเป็น ประเด็นถกเถียงระดับประเทศ ในสหรัฐฯ หลังจากปรากฏในคอลัมน์ของนิตยสารชื่อว่า "Ask Marilyn" ในนิตยสาร Parade ผู้เขียนคอลัมน์คือ Marilyn vos Savant เธอเป็นหญิงสาวที่ได้ชื่อว่ามี IQ สูงที่สุดในโลก (เคยลง Guinness Book) มีคนส่งคำถามเรื่อง Monty Hall ไปถามเธอ
"ถ้าผมเลือกประตู แล้วพิธีกรเปิดอีกประตูที่ไม่มีรางวัล ผมควรเปลี่ยนใจไหม?"
"ควรเปลี่ยน โอกาสชนะจะเพิ่มจาก 1/3→2/3"

คอลัมน์ "Ask Marilyn" โดย Marilyn vos Savant ที่ตอบคำถามเกี่ยวกับปริศนามอนตี ฮอลล์
แต่หลังจากที่ Marilyn vos Savant ตอบคำถามนี้ในปี 1990 ก็ได้มีจดหมายกว่า 10,000 ฉบับเข้ามาโต้แย้งเธอ แม้คำตอบของเธอจะถูกต้องตามหลักคณิตศาสตร์ก็ตาม แม้แต่นักคณิตศาสตร์ระดับอาจารย์มหาวิทยาลัยก็ยังโต้แย้งว่าโอกาสชนะมันควรเป็น 1/2
ปริศนามอนตี ฮอลล์ จึงกลายเป็นตัวอย่างคลาสสิกของ “paradox” ที่ความรู้สึกขัดสามัญสำนึกและตรรกะทางคณิตศาสตร์ แม้แต่นักคณิตศาสตร์ชื่อดัง Paul Erdős ก็ยังไม่เชื่อจนได้เห็นการทดลองจริง
รู้ได้อย่างไรว่าเป็น 2/3 ไม่ใช่ 1/2?
ก่อนอื่นเลย เพื่อที่จะรู้ค่าความน่าจะเป็นของเหตุการณ์หนึ่ง โดยพื้นฐานเราต้องนำ จำนวนเหตุการณ์ที่สนใจ หารด้วย จำนวนเหตุการณ์ทั้งหมดที่เป็นไปได้ (sample space)
ยกตัวอย่างเช่น การทอยลูกเต๋า เมื่อเราสนใจว่าความน่าจะเป็นที่ทอยได้แต้มที่มากกว่า 4 แต้ม
{5, 6} เท่ากับ 2 เหตุการณ์ส่วนจำนวนเหตุการณ์ทั้งหมดคือ
{1, 2, 3, 4, 5, 6} เท่ากับ 6 เหตุการณ์ดังนั้นความน่าจะเป็นคือ
2/6 หรือ 1/3 นั่นเอง ทีนี้เรามาดูกรณีปริศนามอนตี ฮอลล์กันบ้างว่าเกิดอะไรขึ้นเมื่อผู้เล่นเปลี่ยนใจเสมอ การที่จะนับจำนวนเหตุการณ์ลองพิจารณาดังต่อไปนี้

ประตูสามบานที่มีแพะสองตัวกับรถยนต์หนึ่งคัน ผู้เล่นไม่รู้ว่าประตูบานไหนมีอะไรบ้าง
ตอนนี้เรารู้ว่า ประตูสามบานนี้มีแพะสองตัวและรถยนต์อยู่หนึ่งคัน ดังนั้นผลลัพธ์จากการเลือกประตูนั้น มีอยู่สามเหตุการณ์หลัก ๆ คือ
- หลังประตูที่ผู้เล่นเลือก คือ แพะตัวแรก
- หลังประตูที่ผู้เล่นเลือก คือ แพะตัวที่สอง
- หลังประตูที่ผู้เล่นเลือก คือ รถยนต์
ไม่ว่าตำแหน่งของแพะและรถยนต์หลังประตูจะสลับกันอย่างไร เหตุการณ์ที่เกิดขึ้นจะต้องเป็นหนึ่งในสามแบบนี้เสมอ ดังนั้น เราจะไม่สนใจการสลับตำแหน่ง (permutation) ของแพะและรถยนต์ แต่จะพิจารณาแค่ผลลัพธ์จากการเลือกของผู้เล่นก็พอ
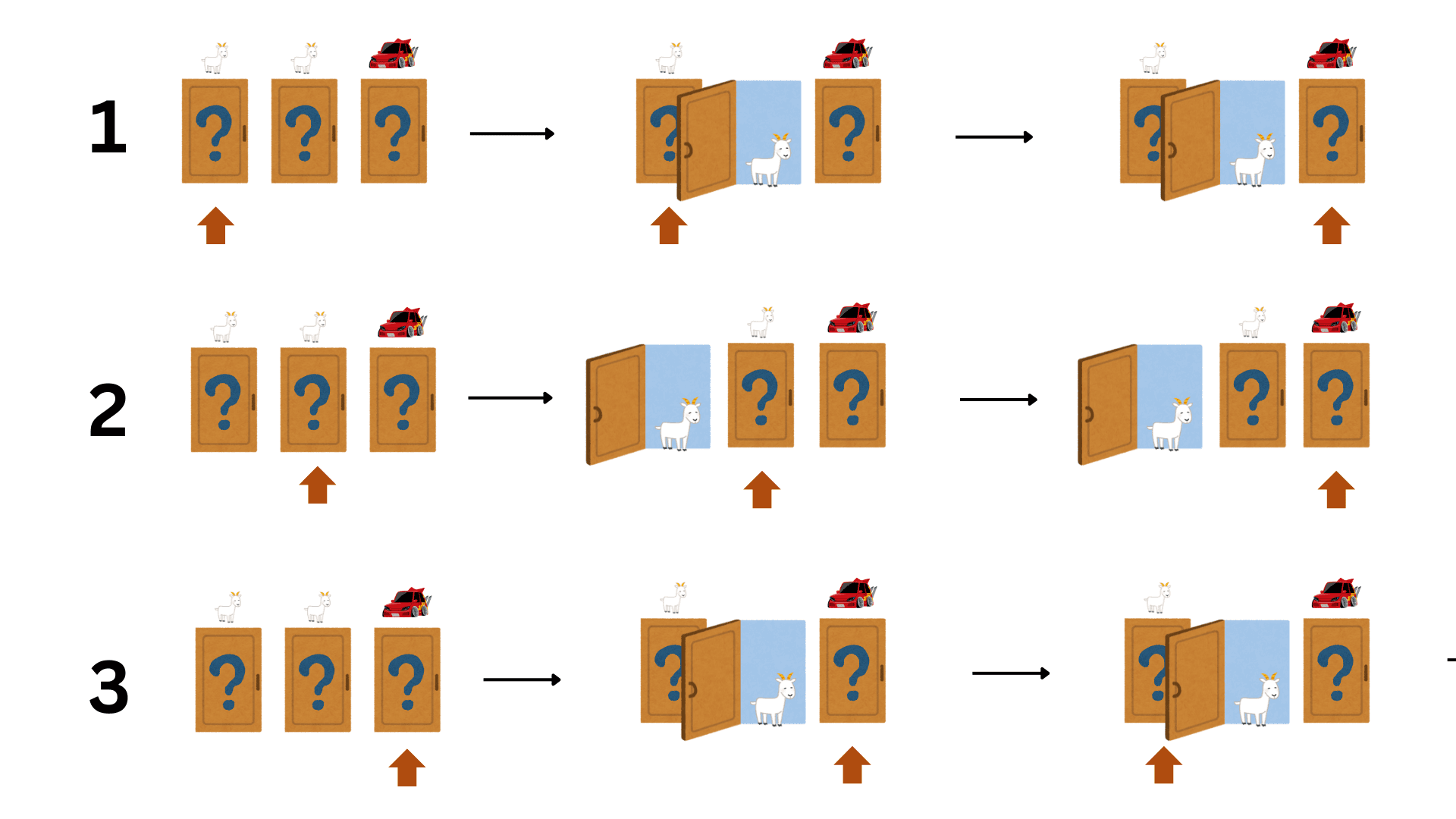
สิ่งที่จะเกิดขึ้นทั้งสามเหตุการณ์หลังจากผู้เล่นเลือกประตู แล้วเปลี่ยนใจ
จากนั้นหลังจากที่ผู้เล่นเลือกแล้ว พิธีกรจะเปิดประตูหนึ่งบานที่มีแพะ จึงทำให้เกิดเหตุการณ์ดังต่อไปนี้
- หลังประตูที่ผู้เล่นเลือก คือ แพะตัวแรก พิธีกรจะเปิดประตูที่มีแพะตัวที่สอง เมื่อผู้เล่นเปลี่ยนใจจะได้รับรถยนต์
- หลังประตูที่ผู้เล่นเลือก คือ แพะตัวที่สอง พิธีกรจะเปิดประตูที่มีแพะตัวแรก เมื่อผู้เล่นเปลี่ยนใจจะได้รับรถยนต์
- หลังประตูที่ผู้เล่นเลือก คือ รถยนต์ พิธีกรจะเปิดประตูบานใดบานหนึ่งที่มีแพะ เมื่อผู้เล่นเปลี่ยนใจจะได้รับแพะอีกตัว
จากเหตุการณ์ที่ 1 และ 2 จะทำให้แพะอีกประตูถูกเปิด และประตูสุดท้ายจะต้องเป็นรถยนต์อย่างแน่นอน ดังนั้นการเปลี่ยนประตูจะทำให้ได้รถยนต์
2/3 ดังนั้น การเปลี่ยนใจจะทำให้มีโอกาสชนะถึง 2/3 แทนที่จะเป็น 1/2 นั่นเองสรุป
ดังนั้นแม้ว่าปริศนามอนตี ฮอลล์จะเป็นปริศนาที่ดูเรียบง่าย คำตอบไม่ซับซ้อน แต่เมื่อเราวิเคราะห์โครงสร้างของเหตุการณ์แล้ว ก็พบว่าจะพบว่า “การเปลี่ยนประตู” หลังจากพิธีกรเปิดประตูหนึ่งบานแล้วนั้น ให้โอกาสชนะมากถึง 2 ใน 3 ซึ่งมากกว่าการเลือกประตูเดิมอย่างมาก
และนี่เองคือสิ่งที่ทำให้ "ความน่าจะเป็น" นั้นเป็นศาสตร์ที่ซับซ้อนและมีเงื่อนไขเยอะ ไม่แปลกเลยว่าทำไมหลายคนถึงยกให้เป็นบทที่เข้าใจยากที่สุดในวิชาคณิตศาสตร์
ความน่าจะเป็น ไม่ใช่แค่เรื่องของการเดา หรือการใช้สามัญสำนึก บางครั้งสิ่งที่ดูเหมือนจะใช่ อาจจะผิดอย่างสิ้นเชิง ในทางกลับกัน สิ่งที่ดูจะเป็นไปไม่ได้ กลับเป็นคำตอบที่ดีที่สุด

